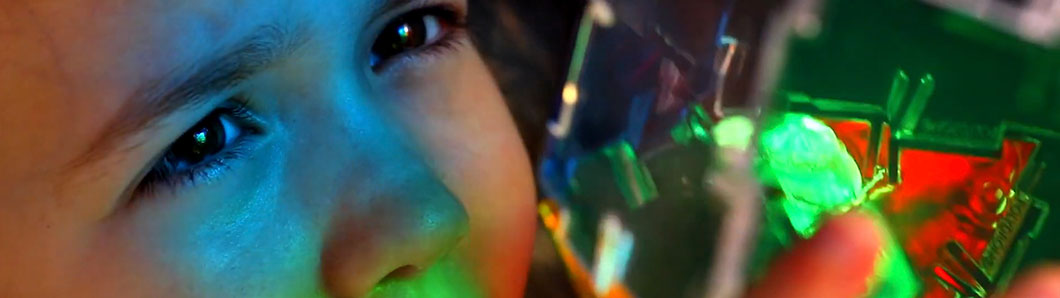Blog

The COP26 summit has further amplified the UK’s commitments to become a world leader in sustainability right across the education system by engaging young people and bringing them on our journey toward net zero and a green future.

Last weekend was my town’s turn to host the Big Draw Festival. The aim of the festival is to encourage children to use drawing as a tool for wellbeing, creativity, and social and cultural engagement.

Play is one of the best ways for young children to develop essential and important tools and skills which will set them up for the rest of their lives. Today, we would like to talk a little bit about light play and how it could benefit your children during their precious time spent playing.

We have a brand new Polydron Cleaning System that will be in stock from the end of October 2021 and is ready to order now!

We are more than often hearing and seeing the benefits of outdoor learning in Early Years settings, so what makes taking the classroom outdoors so good for early years child development? With Outdoor Classroom Day just a few days ago, let’s take a look at the benefits of outdoor activities and a couple of outdoor learning ideas throughout this blog.

The idea for this article came to me whilst I was attempting to open a can of beans, I tried to use the pull ring to get it open, I was trying to manoeuvre my finger underneath to lift it up, but it was one of those pull rings that was tight, and I just couldn’t do it! So, I went to use a can opener instead.

At Polydron, we’ve been working hard on our eco-initiative and we thought with today being Earth Day, there was no better time to share our work with you.

We first discovered Vamsi Poongundran when his parents contacted us to tell us about Vamsi’s passions for STEM and creating engaging content not only for his own personal development but for his peers too. They told us how Vamsi was interested in our fantastic Polydron Bridges and Engineering Sets for an upcoming video.

Christmas is exciting for children (and adults) but why not make maths fun at this time of year, with this quick, simple and fun activity?

Welcome to our quick how to guide on how to construct a Christmas Star! To complete this model, you will need 20 Equilateral Triangles and 10 Squares.