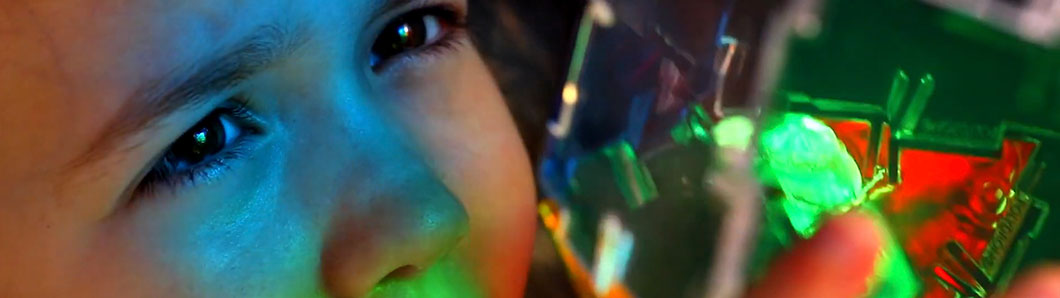This year, Polydron brings you a fantastic new resource for schools and nurseries, suitable from 12 months+. Translucent KinderMag construction set is designed to support mathematical skills, design reasoning, fine motor control, and of course imaginative construction play.
Mathematics
In light of Rishi Sunak asking pupils to study maths until age 18, there's no better time to use Polydron resources in maths problem-solving activities!
As 2021 comes to a close, we can’t help but sit and reflect about all of the things that we achieved this past year. From surviving yet another tumultuous year under a pandemic, to the addition of new members of the team – here are our yearly highlights.
Hang up your tinsel and start warming up the mulled wine – Christmas isn’t cancelled just yet.
The COP26 summit has further amplified the UK’s commitments to become a world leader in sustainability right across the education system by engaging young people and bringing them on our journey toward net zero and a green future.
Play is one of the best ways for young children to develop essential and important tools and skills which will set them up for the rest of their lives. Today, we would like to talk a little bit about light play and how it could benefit your children during their precious time spent playing.
We have a brand new Polydron Cleaning System that will be in stock from the end of October 2021 and is ready to order now!
At Polydron, we’ve been working hard on our eco-initiative and we thought with today being Earth Day, there was no better time to share our work with you.
We first discovered Vamsi Poongundran when his parents contacted us to tell us about Vamsi’s passions for STEM and creating engaging content not only for his own personal development but for his peers too. They told us how Vamsi was interested in our fantastic Polydron Bridges and Engineering Sets for an upcoming video.
Polydron are so happy to announce that 2 of our fantastic products have each won a prestigious Teach Early Years Award in this years competition!