Taking Polydron into the fourth dimension
(For animations go to the Wikipedia entry 'Tesseract'.
To make a straight line, a 1-dimensional shape, we translate a point, a 0-dimensional shape:

To make a square, a 2-dimensional shape, we translate the straight line perpendicular to itself:
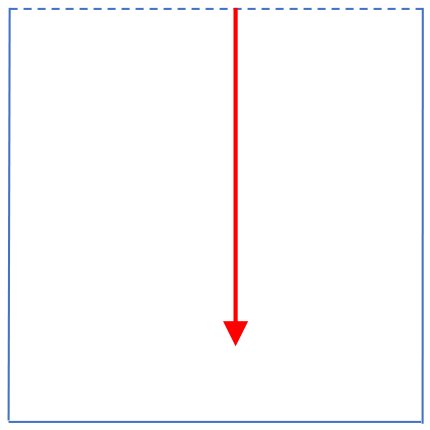
To make a cube, a 3-dimensional shape, we translate the square perpendicular to itself:
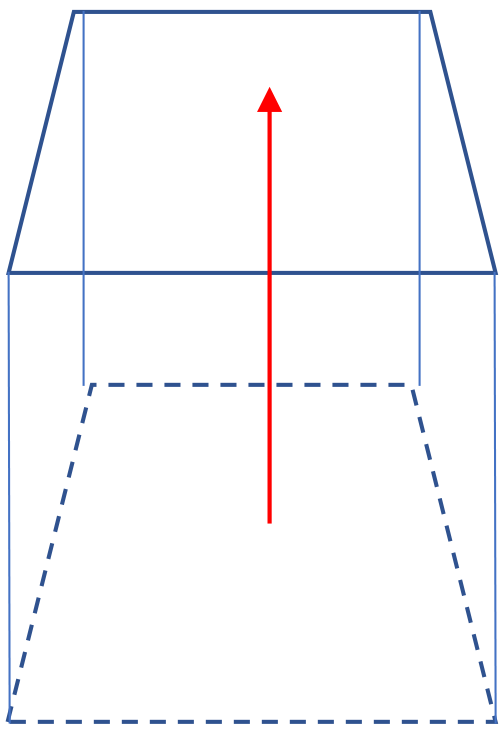
To make a tesseract, a 4-dimensional shape, we translate the cube perpendicular to itself.
- So here comes our 2-D picture of what happens in 4-D to a 3-D shape!
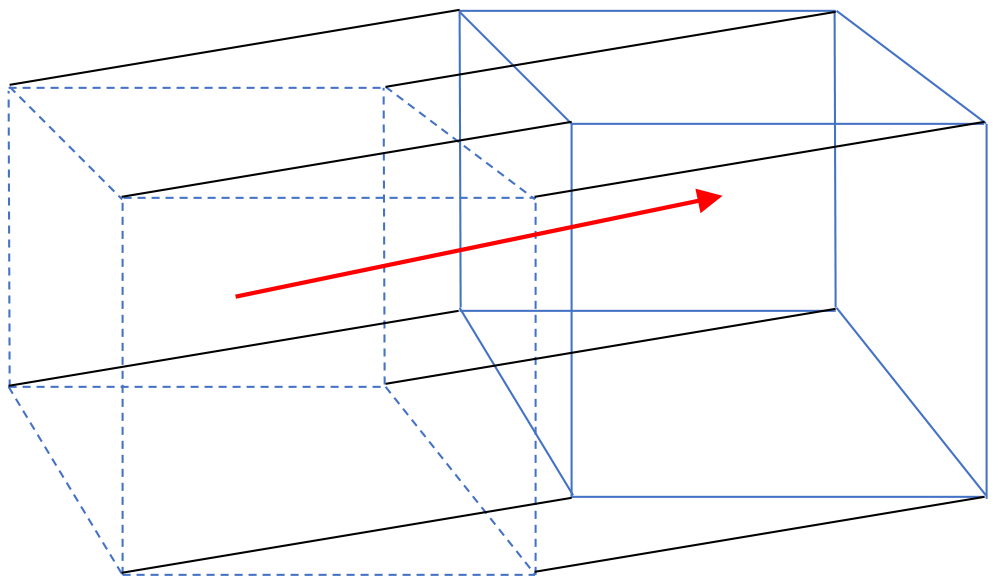
| A cube has: | Dragging it, we end up with: | |
|---|---|---|
| 1 cube | 2(1) + 6 more (one for each face) | = 8 cubes |
| 6 faces | 2(6) + 12 more (one for each edge) | = 24 faces |
| 12 edges | 2(12) + 8 more (one for each vertex) | = 32 edges |
| 8 vertices | 2(8) | = 16 vertices |
We can represent the result more symmetrically as a bubble-in-a-bubble. This cut-away model shows the structure:

Count carefully to check my numbers. (Realise that each volume represents a cube. As you see, there are 6 frusta of pyramids, each extending from a face of the outer bubble to a face of the inner one, making 8 cubes in all.)
As (among others) we can fold this 2-D net in three dimensions to make a cube:

(among others) we can fold this 3-D net in four dimensions to make a tesseract:

As the 2-D net is a polyomino, a shape made by joining squares edge-to-edge, the 3-D net is a polycube, a shape made by sticking cubes face-to-face. Because it features in a famous painting by Salvador Dali, it's called a 'Dali cross'. A special property of this solid is that it is space-filling: you can pack copies together without leaving any gaps. I don't know any other polycube which isn't a prism - a polyomino with thickness - which displays this property.
In this packing the Dali crosses run end-to-end but alternate lines are offset by 2 cubes - I've only used colour to bring out the pattern; the shapes are all the same:

The next picture shows adjacent horizontal layers in a vertical stack. Notice from the red-yellow layer that the holes form a simple grid but the pegs lie in alternate positions in a checkerboard pattern. On the left I've ringed the positions where red and yellow pegs like those on the right stick up through the blue-green layer. This leaves holes to be filled by another set of red and yellow pegs sticking down from the next red-yellow sheet:
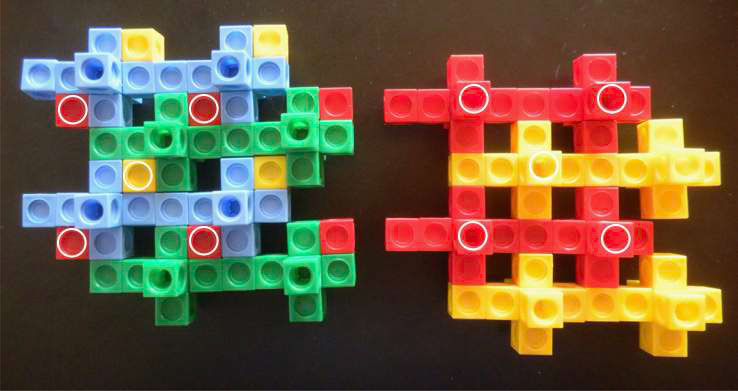
What 4-D shapes fill 4-D space we shall not examine here!
Paul Stephenson, Magic Mathworks Travelling Circus